 .
.유체역팍 관내유동을 보다보니
나온내용에 대해서 궁금한점입니다..
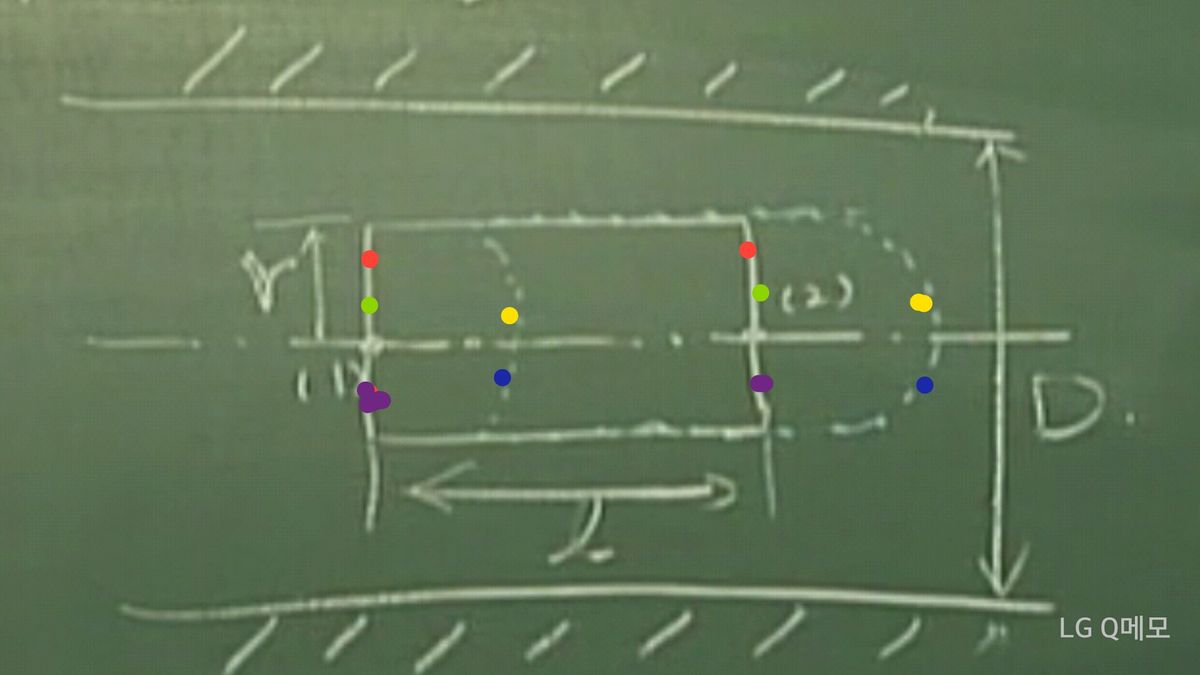
제가 올린 완전발달층류영역에서의 그림파일에서
수직으로 볼때는(y방향) 같은 수직선안에서 압력이 달라질수 있는건 맞는데
X방향의 거리차에 따른 압력차이는
X방향의 거리차이가 같고,
같은 수평선위에있는
두점에서 차이의 크기가 언제나 같다..라고 합니다...
그냥 생각하면 이부분이 말하는게
점성유동이니 근본적으로 파이프로인해 생기는 전단마찰로 소모되는 속도를
압력차이로 메꿔줘서
속도하강없이 정상상태가 유지된다..라고 말하려고 일정거리차에 따른 압력차이는 어디가 되었든 같다고 하려는거같습니다..
그런데 그래도 역시 잘 납득이 가질 않습니다..
이부분 즉 어느위치라도 수평선상의 위치차이(거리)가 같은 두점이라면 언제나 압력차이가 같다.. 라는걸 납득이 가도록 동역학적으로 설명좀 뷰탁드립니다 ㅠㅠ
V2=V1 +integral(a)dt 인데
파이프로인한 점성력 = 압력차로인한 힘
ㄴ이런데 상쇠되서 a=0이라 그럴까요..








댓글 달기